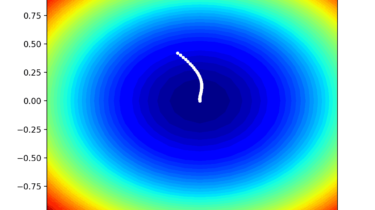
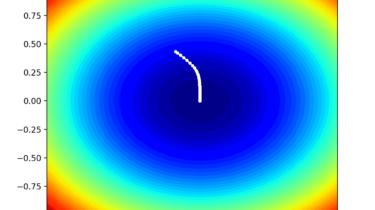
The Broyden, Fletcher, Goldfarb, and Shanno, or BFGS Algorithm, is a local search optimization algorithm. It is a type of second-order optimization algorithm, meaning that it makes use of the second-order derivative of an objective function and belongs to a class of algorithms referred to as Quasi-Newton methods that approximate the second derivative (called the Hessian) for optimization problems where the second derivative cannot be calculated. The BFGS algorithm is perhaps one of the most widely used second-order algorithms for […]

Dual Annealing is a stochastic global optimization algorithm. It is an implementation of the generalized simulated annealing algorithm, an extension of simulated annealing. In addition, it is paired with a local search algorithm that is automatically performed at the end of the simulated annealing procedure. This combination of effective global and local search procedures provides a powerful algorithm for challenging nonlinear optimization problems. In this tutorial, you will discover the dual annealing global optimization algorithm. After completing this tutorial, you […]

Gradient descent is an optimization algorithm that follows the negative gradient of an objective function in order to locate the minimum of the function. A limitation of gradient descent is that it uses the same step size (learning rate) for each input variable. AdaGrad, for short, is an extension of the gradient descent optimization algorithm that allows the step size in each dimension used by the optimization algorithm to be automatically adapted based on the gradients seen for the variable […]

The line search is an optimization algorithm that can be used for objective functions with one or more variables. It provides a way to use a univariate optimization algorithm, like a bisection search on a multivariate objective function, by using the search to locate the optimal step size in each dimension from a known point to the optima. In this tutorial, you will discover how to perform a line search optimization in Python. After completing this tutorial, you will know: […]

Function optimization is a field of study that seeks an input to a function that results in the maximum or minimum output of the function. There are a large number of optimization algorithms and it is important to study and develop intuitions for optimization algorithms on simple and easy-to-visualize test functions. One-dimensional functions take a single input value and output a single evaluation of the input. They may be the simplest type of test function to use when studying function […]

Function optimization is a foundational area of study and the techniques are used in almost every quantitative field. Importantly, function optimization is central to almost all machine learning algorithms, and predictive modeling projects. As such, it is critical to understand what function optimization is, the terminology used in the field, and the elements that constitute a function optimization problem. In this tutorial, you will discover a gentle introduction to function optimization. After completing this tutorial, you will know: The three […]

Machine learning involves using an algorithm to learn and generalize from historical data in order to make predictions on new data. This problem can be described as approximating a function that maps examples of inputs to examples of outputs. Approximating a function can be solved by framing the problem as function optimization. This is where a machine learning algorithm defines a parameterized mapping function (e.g. a weighted sum of inputs) and an optimization algorithm is used to fund the values […]

Convergence refers to the limit of a process and can be a useful analytical tool when evaluating the expected performance of an optimization algorithm. It can also be a useful empirical tool when exploring the learning dynamics of an optimization algorithm, and machine learning algorithms trained using an optimization algorithm, such as deep learning neural networks. This motivates the investigation of learning curves and techniques, such as early stopping. If optimization is a process that generates candidate solutions, then convergence […]

Gradient descent is an optimization algorithm that follows the negative gradient of an objective function in order to locate the minimum of the function. A limitation of gradient descent is that a single step size (learning rate) is used for all input variables. Extensions to gradient descent, like the Adaptive Movement Estimation (Adam) algorithm, use a separate step size for each input variable but may result in a step size that rapidly decreases to very small values. AdaMax is an […]

Gradient descent is an optimization algorithm that follows the negative gradient of an objective function in order to locate the minimum of the function. A limitation of gradient descent is that a single step size (learning rate) is used for all input variables. Extensions to gradient descent like the Adaptive Movement Estimation (Adam) algorithm use a separate step size for each input variable but may result in a step size that rapidly decreases to very small values. AMSGrad is an […]