A Gentle Introduction to Information Entropy
Last Updated on July 13, 2020
Information theory is a subfield of mathematics concerned with transmitting data across a noisy channel.
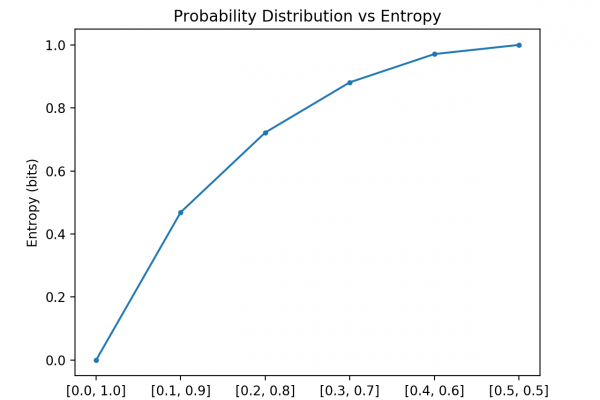
A cornerstone of information theory is the idea of quantifying how much information there is in a message. More generally, this can be used to quantify the information in an event and a random variable, called entropy, and is calculated using probability.
Calculating information and entropy is a useful tool in machine learning and is used as the basis for techniques such as feature selection, building decision trees, and, more generally, fitting classification models. As such, a machine learning practitioner requires a strong understanding and intuition for information and entropy.
In this post, you will discover a gentle introduction to information entropy.
After reading this post, you will know:
- Information theory is concerned with data compression and transmission and builds upon probability and supports machine learning.
- Information provides a way to quantify the amount of surprise for an event measured in bits.
- Entropy provides a measure of the average amount of information needed to represent an event drawn from a probability distribution for a random variable.
Kick-start your project with my new book Probability for Machine
To finish reading, please visit source site